Soft hydraulic module

The soft hydraulic module of the WaterSed model can simulate four types of soft hydraulics : fascine, hedge, grass strip and pond/buffer basin.

1. Hydrological functioning

Each soft hydraulics is described using 4 parameters.

• Width (m)
• Infiltration capacity (mm/h)
• Manning’s coefficient (s.m^-1/3)
• Volume (m³)

Incorporating soft hydraulics into the model involves modifying the input grids of the model, on the cells where the soft hydraulics are located.

Infiltration capacity.

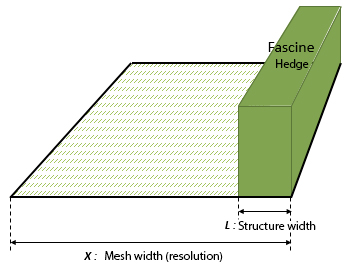
The final infiltration capacity IC’_i (mm/h) is calculated proportionaly structure width structure L and the DTM resolution X.

If the width of the structure is less than the resolution of the DTM :

With :

IC_i : initial infiltration capacity of mesh i (mm/h)

IC_AMGi : infiltration capacity of the layout (mm/h)

L : width of the layout (m)

X : DTM resolution (m)

If the width of the structure is greater than or equal to the resolution of the DTM, then :

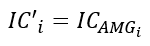
This method is applied to all soft hydraulics : fascine, hedge, grass strip and pond/buffer basin.

Imbibition

For a fascine, hedge or grass strip mesh, the final imbibition IMB’_i (mm) is that of the initial imbibition grid IMB_i (mm), used as model input :

For a pond/buffer basin cell, the initial imbibition value IMB_i (mm) is replaced by the structure volume VO_i (mm). This numerical trick makes it possible to artificially dig a well which volume is that of the structure.

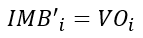
Water storage capacity of the soil

For a fascine, hedge or grass strip cell, the final soil water storage capacity WS’_i is that of the initial soil water storage capacity WS_i (mm), provided as input to the model.

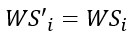
For a pond/buffer basin cell, the final soil water storage capacity WS’_i (mm) is the sum of the initial soil water storage capacity WS_i (mm) and the volume of the structure VO_i (mm).

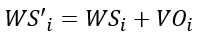
Manning’s coefficient

For the four types of soft hydraulics, the final Manning coefficient n’_i corresponds to the Manning coefficient of the layout n_AMGi.

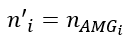
2. Sedimentary functioning

For the four types of soft hydraulics, the concentration of SPM in runoff water SPM_i (g/l) and the erodibility EROD_i (-) is equal to 0.

Fascine / Hedge

For fascines and hedges, an empirical equation has been developed on the basis of AREAS work. The sediment transfer rate T_Ti (-) is a function of the specific water inflow Q_Si (m³/m/s). The equation is as follows :

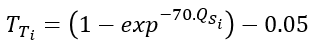
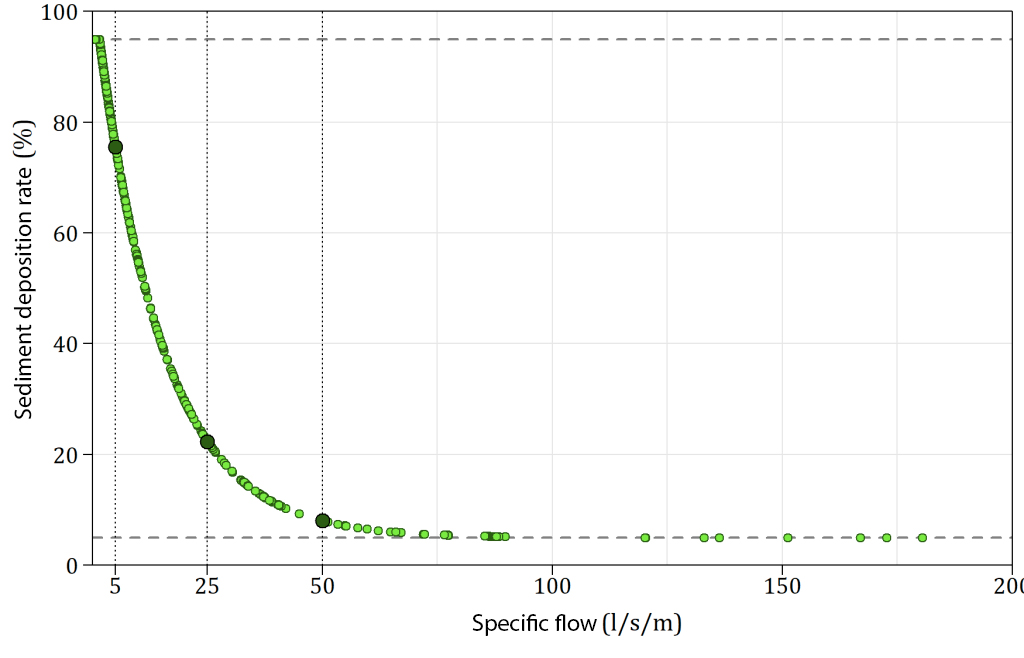
The transfer rate was bounded between 0.05 and 0.95 since these structures can’t trap/transfer 100% of the sediment flux. Based on this transfer rate, the sediment deposition rate T_Di (-) is determined according to the equation :

The relation is shown in the figure below. The greater the specific inflow Q_Si, the lower the sediment deposition rate T_Di is.

Pond / Buffer basin

The sediment transfer rate of a basin is a function of the volume of runoff V_i (m³) entering the structure.

If the volume of runoff leaving the structure V_i (m³) is greater than the storage volume of the structure VO_i (m³), the sediment transfer rate T_Ti (-) is :

If the runoff volume V_i (m³) is less than or equal to the storage volume of the structure VO_i (m³), the sediment transfer rate T_Ti (-) is equal to 0.

Grass strip

The sediment transfer rate of a grass strip is determined using the model’s transport capacity equation. Increasing the Manning’s coefficient across a grass strip (between 0.15 and 0.3) reduces the transport capacity and thus increases sediment deposition.